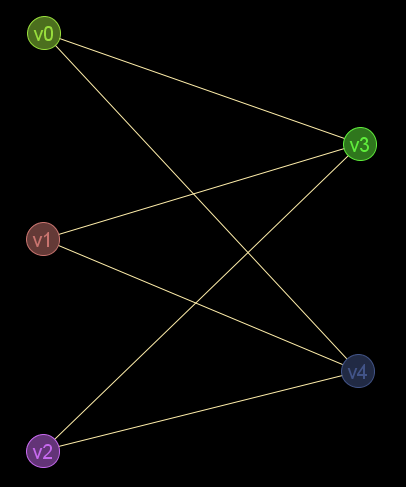
Grafo no dirigido de 5 nodos:
gr_nuevo([[0,0,0,1,0],[0,0,0,1,0],[0,0,0,0,1],[1,1,0,0,0],[0,0,1,0,0]],falso)
Salida JMEScriptGUI con visor de grafos v0.1:
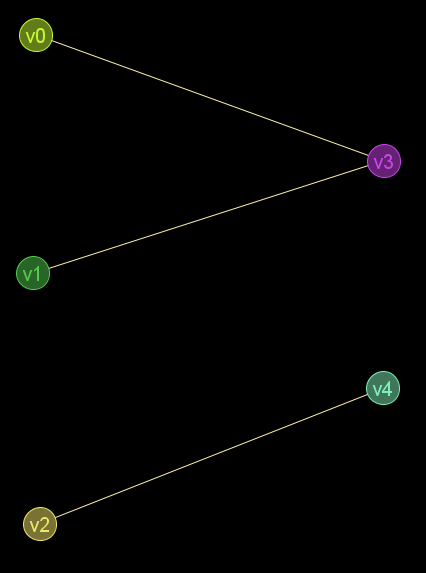
gr_bipartito(gr_nuevo([[0,0,0,1,0],[0,0,0,1,0],[0,0,0,0,1],[1,1,0,0,0],[0,0,1,0,0]],falso))
VectorEvaluado: [[0,1,2],[3,4]]
Comprobar si el grafo anterior es bipartito completo:Salida en REPL:
>>> set g=gr_nuevo([[0,0,0,1,0],[0,0,0,1,0],[0,0,0,0,1],[1,1,0,0,0],[0,0,1,0,0]],falso)|| >>> set particion=gr_bipartito(g) particion ==> VectorEvaluado: [[0,1,2],[3,4]] (parse: 112µs(8%) / eval: 1,2ms(92%) / total: 1,3ms) >>> dim(particion><0)*dim(particion><1)=gr_numaristas(g) ==> Booleano: falso (parse: 993µs(45%) / eval: 1,2ms(55%) / total: 2,2ms) >>>